Introduction

Il y a quelques temps, sur LinkedIn, une question est apparue dans mon fil de discussion : comment géreriez-vous la recherche de similarité de parcours réalisés par des véhicules et enregistrés sous la forme de traces GPS? L’auteur insistait sur le besoin d’un algorithme et d’une structure de données efficaces, pour d’une part être robuste aux erreurs de coordonnées propres aux traces GPS, et d’autre part pour gérer un nombre potentiellement élevé de points.

Bref: comment déterminer la similarité entre deux traces GPS?

La discussion s’est avérée être un piège à click, avec une relance de l’auteur au bout de quelques jours, du type « Je vous ai bien eu: en réalité les traces se résument souvent à un point de départ et un point d’arrivée. Vos solutions sont plus complexes que nécessaires. »

Passons sur le problème mal posé. La question demeure, et je m’y suis intéressé.

Le problème

Un aspect important du problème vient de ce qu’une trace GPS est une séquence de coordonnées. Chaque coordonnée est une paire de valeurs représentant la latitude et la longitude du véhicule à un moment donné. Un système GPS a une précision typique comprise entre 1 et 10 mètres. De plus, même si la précision spatiale était parfaite, relever la position à des moments différents mène à des coordonnées différentes. On ne peut donc comparer strictement les coordonnées. D’où le besoin d’une notion de similarité.

On souhaite comparer des traces relatives à des véhicules différents, roulant à des moments différents. La dimension temporelle est donc presque totalement omise: seul l’ordre des coordonnées est potentiellement pertinent.

Déterminer la similitude entre plusieurs traces, ou trouver les traces présentant une similitude avec une trace donnée, présente plusieurs intérêts. Premièrement, et c’était l’objectif dans la discussion à l’origine de ma réflexion, cela permet de récupérer des résultats obtenus sur des traces historiques et qu’on espère être à nouveau pertinents. De nombreux algorithmes prédictifs se basent sur une notion de similarité pour établir leurs predictions. La similarité peut également être à la base d’une détection d’anomalie, par exemple pour prévenir un bus ou un randonneur qui se fourvoie, ou encore pour identifier un taxi qui emprunte des détours sans bonne raison. La détection d’anomalies sur les trajets routiers permet de repérer des obstacles à la circulation ou, inversement, l’ouverture de voies qui ne figurent pas sur la carte.

Le repérage de traces similaires peut servir à l’amélioration de l’infrastructure ou des services sur les accès fréquentés. On peut organiser un transport collectif ou améliorer les transports en communs.

Discrétisation des coordonnées

Puisque les coordonnées ne sont enregistrées qu’avec une précision relative, une mesure directe de leur distance (par exemple avec la distance de Hausdorff) serait fort sensible au bruit des relevés, tout en présentant un coût de traitement élevé.

Une approche alternative consiste à découper le monde en « cases », par exemple des carrés de 100 mètres de côté. On remplace chaque coordonnée par la case à laquelle elle correspond. On espère ainsi que les imprécisions des coordonnées seront gommées par la granularité du quadrillage: deux coordonnées similaires devraient souvent avoir la même case. On revient alors à la comparaison stricte de deux séquences de valeurs.

Cette approche simplifie le problème, mais souffre d’imperfections. Premièrement, deux coordonnées proches du bord d’une case risquent de se retrouver dans deux cases distinctes. Ensuite, selon l’enregistrement réalisé, il est possible que certaines cases soient « sautées » (par exemple, si le véhicule roule vite par rapport à la résolution du quadrillage). Enfin, on souhaite considérer les petites alternatives de route (une déviation, par exemple).

Bien qu’ayant atténué le problème de l’imprécision spatiale, notre approche par case ne l’a donc pas fait disparaître, si bien qu’une comparaison stricte des séquences de cases n’est pas appropriée.

Calcul de similarité à partir des cases

Afin de pallier à l’approximation persistante de la discrétion de l’espace, on peut considérer les éléments suivants.

Premièrement, l’ordre des cases au sein d’une trace n’est pas très pertinent: sur un trajet donné, l’ensemble des cases fournit pratiquement la même information que leur séquence, pour autant que le véhicule ne fasse pas de boucle, marche arrière, ou autre manœuvre de ce type. Tout au plus souhaite-t-on conserver la direction générale d’une trace (par exemple du nord au sud) afin de distinguer un trajet aller du retour.

Ensuite, le nombre de cases communes entre deux traces est un bon indicateur de leur similarité. On peut donc mesurer cette similarité par l’indice de Jaccard des cases de deux traces.

Structure de données

Afin de permettre la récupération rapide et efficace des traces historiques présentant une similarité importante avec une trace quelconque, on peut s’inspirer du travail de Shazam, qui vise à récupérer les musiques similaires à un extrait proposé.

D’une part, on associe à chaque trace enregistrée la liste des cases, préalablement calculée. D’autre part, on associe à chaque case considérée la liste des traces comportant cette case. Notez que ces deux associations ont potentiellement une grande cardinalité: la première aura autant d’entrées que de traces considérées, tandis que la seconde aura autant d’entrées que de cases traversées par au moins une trace.

Lorsqu’une trace est soumise au système, on détermine les cases qui lui sont associées. On utilise la seconde association pour déterminer l’ensemble des traces étant associées à chacune des cases de la trace considérées. On compte le nombre de fois que chaque trace est ainsi répertoriée. Les traces les plus souvent présentes ont le plus de chance de présenter une bonne similarité avec la trace de référence.

Pour quantifier leur similarité, on considère soit l’ensemble des traces identifiées, soit seulement les meilleures candidates. On récupère leurs cases grâce à la première association, et on calcule l’index de Jaccard entre ces cases et celles de la trace de référence.

Notez que toutes ces actions peuvent être facilement parallélisées et distribuées.

Selon l’ampleur du projet, la structure de données pourra simplement être un dictionnaire en mémoire ou une base de données relationnelle. Une base de données supportant nativement les listes d’objets pourrait s’avérer pratique et efficace. Enfin, notons que le modèle de données de Cassandra se prête très bien à notre problème.

Vers un pattern plus spécifique

Un inconvénient de l’approche discutée est que certaines cases sont « populaires »: elles sont associées à de nombreuses traces, ce qui mène à un comptage important. Imaginez par exemple une case couvrant une autoroute importante ou celle couvrant la place Charles-de-Gaulle à Paris.

Shazam peut à nouveau nous inspirer afin de réduire ce problème : plutôt que de considérer les cases séparément, tentons de dégager un schéma d’un ensemble de cases temporellement liées. Dans notre cas, nous pourrions considérer les séquences de 2, 3, … cases consécutives et associer non pas les cases elles-mêmes, mais ces courtes séquences, aux traces qui les comportent. En pratique, on calculera le hachage roulant des N cases consécutives d’une trace, et on mémorisera la relation entre chacun de ces hachages et la trace.

Le volume total des données n’est pas grandement impacté par ce changement. Par contre, on peut espérer que les hachages seront plus spécifiques, puisqu’ils mettent en évidence de courtes successions de cases communes à plusieurs traces. A minima, le sens de déplacement est implicitement ajouté. À un embranchement routier, on ne considère plus une route unique, mais aussi la bifurcation empruntée.

Une approche similaire est parfois adoptée par les outils de détection de clones dans les bases de code source.

Un inconvénient de cette approche est qu’un élément de similitude entre deux traces ne sera considéré que si la séquence de longueur N se retrouve sur les deux traces. Étant donnée l’imprécision de la discrétisation spatiale que nous réalisons, il est possible que certaines séquences ne soient pas identiques auprès de traces similaires. Il faut ici espérer que les traces similaires auront suffisamment de séquences communes pour se démarquer. En terme de recherche, il me semble intéressant d’étudier l’impact de l’utilisation de hachages roulant, tant sur la spécificité des traces récupérées que sur la perte de précision que cela occasionne.

De la case au segment

Une amélioration de notre approche consiste à partir d’une discrétisation spatiale de meilleure qualité. Nous visons une réduction de l’imprécision et une granularité spatiale plus subtile que celle proposée par un simple quadrillage.

Le map matching permet une telle amélioration. Il s’agit de considérer le réseau routier comme un graphe dont les nœuds sont les intersections de route, et les arêtes (appelés segments) sont les sections de route reliant deux intersections. Les traces doivent alors être traitées, afin de transformer leurs séquences de coordonnées en séquences de segments.

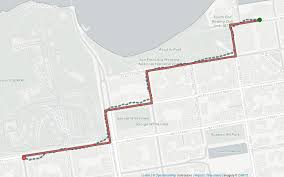
Cela ramène les coordonnées à un système topologique bien défini, ce qui réduit l’imprécision spatiale.

La granularité spatiale est beaucoup plus intelligente: on n’utilise qu’un segment pour un tronçon d’autoroute de plusieurs kilomètres, tant qu’il ne presente ni entrée ni sortie. Inversement, les petites bifurcations sont précisément prises en compte.

Au-delà de cette transformation, qui présente son lot de difficultés, ce raffinement est techniquement facile à intégrer: on peut reproduire l’ensemble de notre approche en remplaçant simplement le concept de case par celui de segment. Lors du calcul de similarité entre deux traces, il peut être intéressant de pondérer les segments afin d’accorder plus d’importance à un segment représentant 2 km d’autoroute qu’à une rue de 200 mètres.

Jeu de données

Si vous souhaitez creuser le sujet par l’expérimentation, je vous recommande le jeu de données officiel des déplacements de taxis new-yorkais. Il a été utilisé dans de nombreuses études, notamment afin d’identifier des trajets anormaux.

Conclusion

Pour autant qu’on s’attaque à une version non triviale de ce problème, la recherche de similitudes dans des traces GPS présente de nombreux défis. Alors que pratiquement tout ce qui roule, marche, vole ou navigue est équipé d’un besoin système de localisation, il faut une solution pouvant passer à l’échelle.

Par cet article, j’ai voulu présenter l’approche qui m’est venue à l’esprit. Elle s’inspire de travaux que j’ai pu lire dans des domaines similaires et d’idées que j’ai pu avoir dans le passé sans avoir eu l’occasion de les développer.