Introduction

Vilfred Pareto est un économiste italien du 19e et début du 20e siècle, principalement connu pour le principe qui porte son nom et qui est une généralisation de l’observation selon laquelle 20 % de la population italienne (de son temps) possède 80 % des richesses nationales.

Dans cet article, nous nous intéressons à un concept qui porte également son nom, et dont la connaissance peut s’avérer utilise dans des contextes très variés: le front (de) Pareto.

Présentation

Imaginez que vous ayez à choisir une nouvelle voiture. Seuls deux critères comptent pour vous: sa vitesse maximale et sa consommation nominale. Pour simplifier les choses, nous mesurerons la vitesse maximale en km/h, et la consommation nominale en kilomètres par litre (à la mode anglo-saxonne, donc: une consommation de 5l/100 km étant équivalente à 20 km/l). Cette dernière unité est peu courante chez nous. Si elle ne change rien à notre réflexion, elle permet d’avoir deux critères de type « plus c’est grand, mieux c’est », ce qui facilite notre compréhension.

On souhaite donc choisir, parmi tout un éventail de modèles de voitures, celle qui est à la fois la plus rapide et celle la plus économe en carburant.

Création du front de Pareto

Commençons par considérer deux voitures, A et B. A a une vitesse maximale de 130 km/h et une consommation de 20 km/l. B a une vitesse maximale de 120 km/h et une consommation de 15 km/l. A est meilleure que B sur tous les critères que nous considérons: on dit que A domine B.

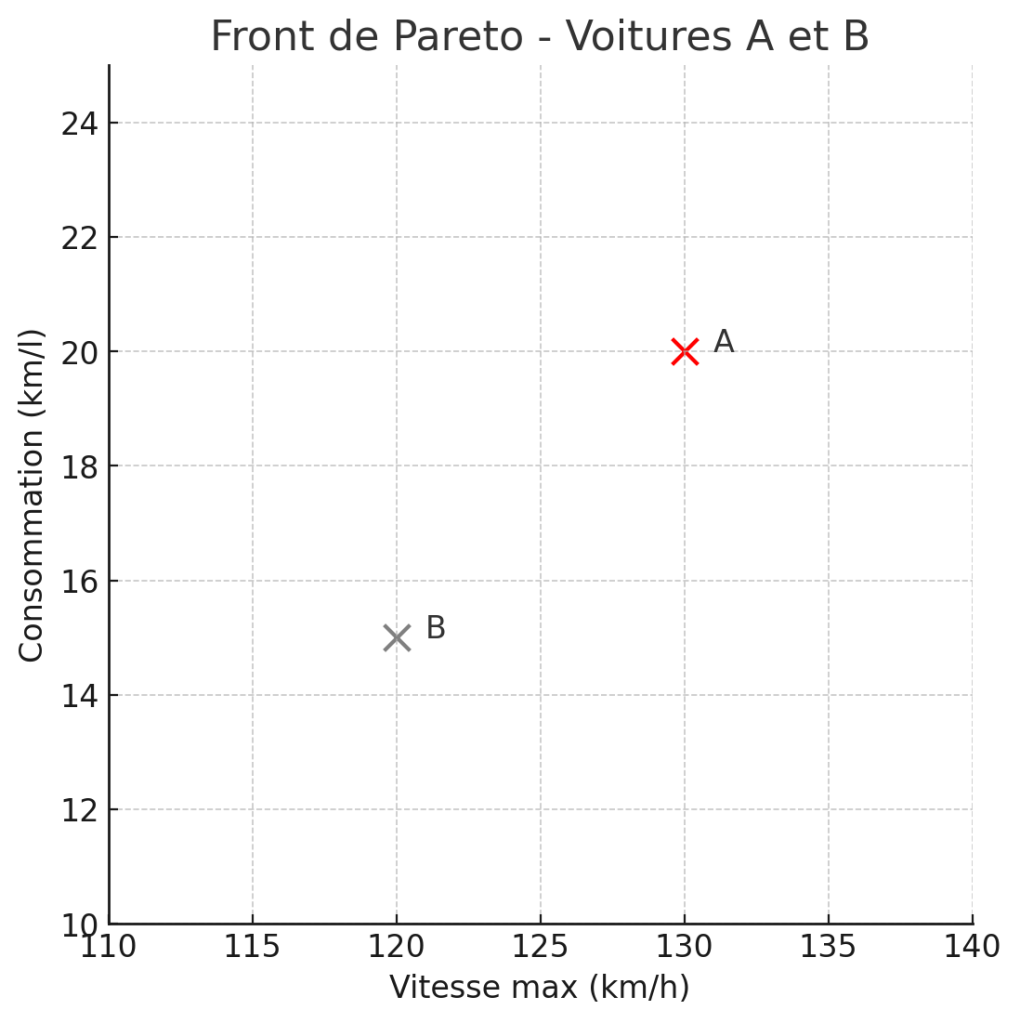
Considérons une troisième voiture C, avec une vitesse maximale de 140 km/h et une consommation de 17 km/l. C est donc meilleure que A en termes de vitesse, mais en même temps moins bonne en termes de consommation. Choisir entre A et C est donc une affaire de compromis; on ne peut exclure ni A ni C de notre « short list » des meilleures voitures puisqu’aucun ne domine l’autre.

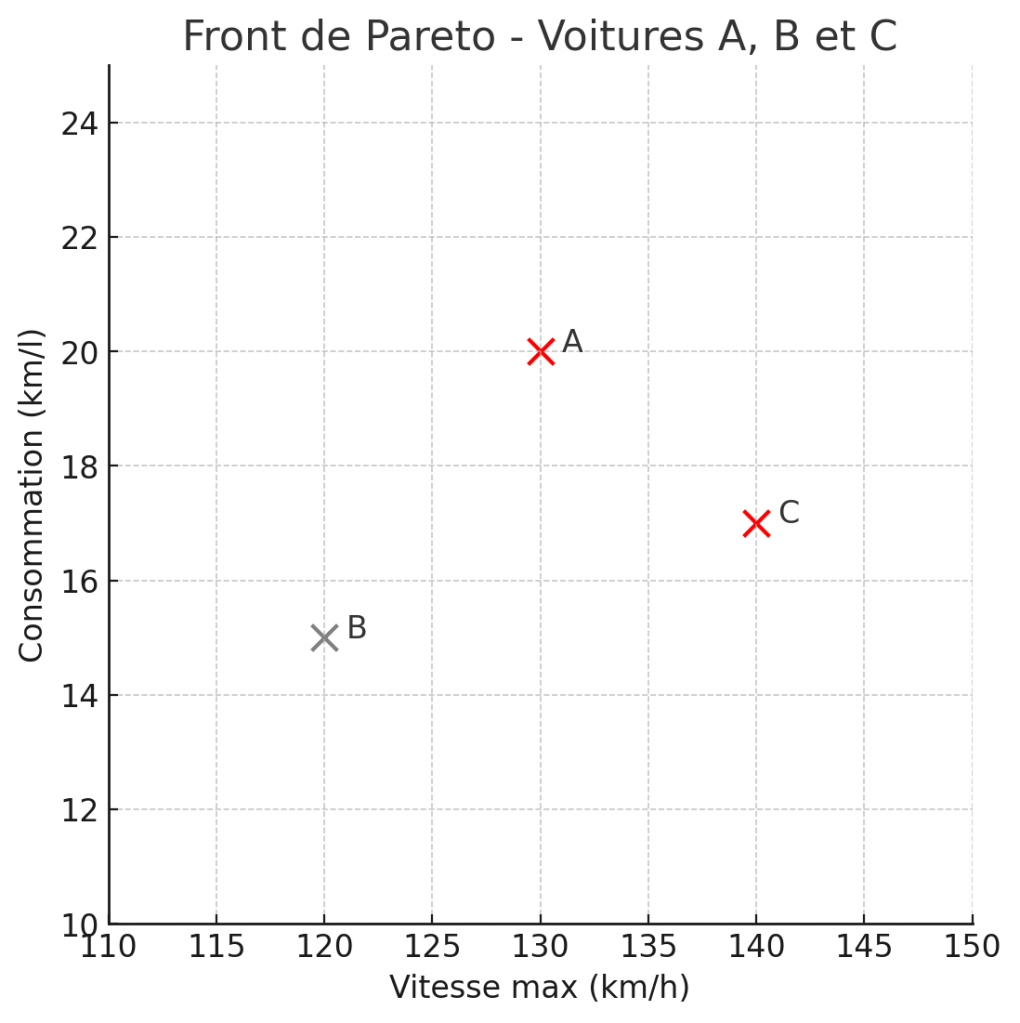
Le front Pareto (ou frontière de Pareto) est précisément constitué de cette « short list »: il s’agit du sous-ensemble des éléments qui sont dominés par aucun autre point. Inversement, un élément est exclu du front de Pareto s’il est dominé par au moins un autre élément. Le terme de « front » vient de ce que, représentés visuellement, les éléments efficaces se trouve en bordure de l’ensemble des éléments considérés.

Notez que ce front est relativement instable. Il peut suffire d’ajouter ou de retirer un élément de l’ensemble considéré pour le modifier considérablement. Par exemple, si nous considérons une voiture D ayant une vitesse maximale de 150 km/h et une consommation de 25 km/l, nous remarquons que D domine A et C. Ces deux voitures ne font alors plus partie du front de Pareto, et seule D subsiste dans le front.

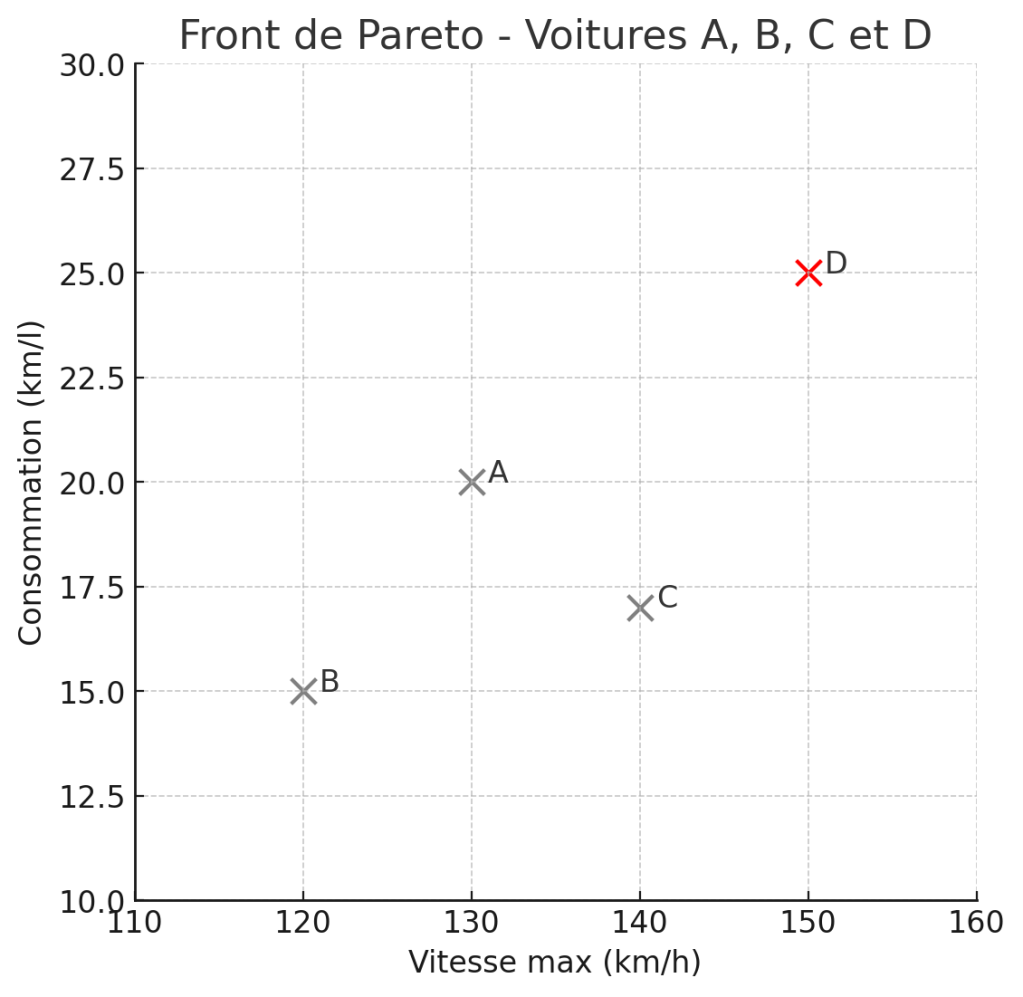
Malédiction de la dimensionnalité

Le critère d’optimalité de Pareto est très flexible: les critères de comparaison peuvent être de nature très variable (des vitesses, des consommations, des prix, …) et porter sur des unités d’échelle très différentes (une centaine de km/h, quelques dizaines de km/l, quelques dizaines de milliers d’euro). On peut donc créer des fronts de Pareto en utilisant pratiquement n’importe quel type de critère, pour autant qu’il existe une relation d’ordre sur ce critère.

Néanmoins, ajouter des critères tend à réduire la pertinence du caractère optimal des éléments. Par exemple, si nous ajoutons le MTBF des voitures (c’est-à-dire le temps moyen entre deux pannes), le compromis devient plus subtil: il est plus probable qu’une voiture parvienne à rester dans le front Pareto, en présentant une vitesse maximale moindre et une consommation plus élevée que d’autres véhicules, mais aussi un MTBF plus élevé que celui des autres voitures. Si on ajoute encore le prix, une voiture pourrait rester dans le front en dépit d’une vitesse maximale faible, d’une consommation plus importante et d’un MTBF réduit, grâce à un coût plus réduit. Au fur et à mesure que de tels critères sont ajoutés, il est de plus en plus difficile pour un élément de dominer les autres, et une part de plus en plus importante de l’ensemble considéré se trouve dans le front Pareto.

C’est d’ailleurs une technique commerciale classique: les sociétés multiplient les spécificités de leurs produits ou services, si bien qu’une comparaison avec les produits ou services de la concurrence est peu productive.

Afin de limiter ce problème, on peut tenter de réduire le nombre de critères considérés, par exemple en les rendant substituables les uns aux autres. Pour nos voitures, on peut par exemple observer que la vitesse maximale et la consommation moyenne d’une voiture ne sont pas indépendants, mais que l’une est inversement proportionnelle à l’autre. On pourrait également dire dans quelle mesure un acheteur est prêt à payer plus pour avoir une voiture plus rapide.

Malheureusement, en pratique, cela est difficile, car les relations entre les critères (quand elles existent) sont rarement linéaires. Par exemple, un acheteur paiera volontiers plus cher pour avoir une voiture qui roule à une vitesse « décente », mais ne sera pas prêt à payer plus pour que la vitesse maximale de sa voiture passe de 200 km/h à 210 km/h.

Par ailleurs, les critères eux-mêmes peuvent être non linéaires. Par exemple, un acheteur peut avoir un budget limité pour sa voiture. Il ne pourra donc substituer librement le coût avec les autres critères.

Selon les circonstances, un algorithme de réduction de la dimensionnalité, tel qu’une analyse en composantes principales, ou l’application d’un auto-encodeur peut aider à réduire le nombre de dimensions considérées.

Un décideur peut avoir du mal à décider de la sélection d’un individu lorsque le front Pareto est constitué d’un grand nombre d’éléments. Cet ensemble peut être restreint à une dizaine d’éléments par exemple, pour autant que ces éléments représentent des compromis suffisamment différents les uns des autres. Une manière de parvenir à ce résultat consiste à appliquer un algorithme de clustering qui réduit l’ensemble à quelques clusters, puis ne présenter, pour chaque cluster, qu’un élément représentatif. L’algorithme K-Means, appliqué en utilisant non pas les attributs des éléments mais leurs valeurs dans l’espace des critères, peut s’avérer utile dans ce cas.

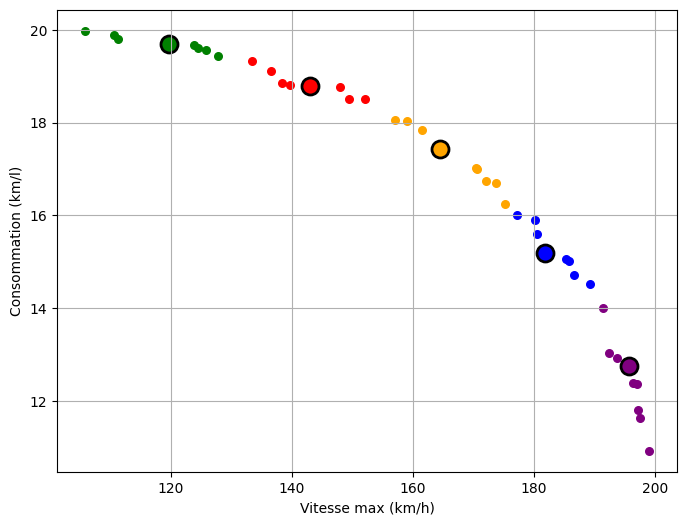
De la difficulté d’établir un front Pareto

Étant donnée la simplicité de sa définition, il peut sembler que déterminer le front Pareto d’un ensemble soit simple. Il s’agit essentiellement de trier les éléments de cet ensemble, selon un ordre partiel reposant sur d dimensions. Cela se fait en O(n²d) dans le pire des cas. Ça pique.

Les choses se corsent encore lorsque l’évaluation d’un élément est coûteuse ou que ces éléments sont très nombreux, voire illimités. C’est le cas par exemple lorsque chaque élément représente un paramétrage possible d’un processus industriel, et que les valeurs des critères d’évaluation ne sont connues qu’une fois ce processus terminé. Il faut alors des stratégies d’exploration du front Pareto aussi efficaces que possible.

La littérature est abondante à ce sujet, car le problème reste ouvert. Relevons simplement qu’on peut avoir recours à des heuristiques d’optimisation qui remplacent la véritable évaluation des éléments par l’usage d’un modèle de machine learning prédictif approximant cette évaluation. 

À noter également, l’algorithme S-Metric Selection Evolutionary Multi-Objective (à vos souhaits) qui consiste en une approche évolutionniste tentant de maximiser le volume de l’espace des éléments. Elle donne la priorité à des individus qui maximisent le volume exploré, ce qui permet de le « ratisser » plus rapidement.

Conclusion

Le front Pareto est un terme qui cache un concept relativement simple et utile dans de nombreux contextes. À défaut de briller lors de soirées mondaines, vous pourrez l’utiliser professionnellement pour décrire de manière univoque les situations présentant une forme d’optimum lorsque plusieurs dimensions de comparaison sont en jeu.

Dans de nombreuses circonstances, il n’est pas possible de calculer explicitement un front Pareto, que ce soit parce que les candidats sont trop nombreux, leur évaluation trop coûteuses, ou parce que travailler avec un front exhaustif n’aide pas beaucoup à la prise de décision. Il existe de nombreuses techniques, issues des procédés d’optimisation, du machine learning ou du data mining, qui permettent de se ramener à une situation plus concrète et plus utile.

Que vous envisagiez d’acheter une voiture, optimiser un procédé industriel ou mettre au point de nouveaux médicaments, le traitement automatique du front de Pareto vous permettra de faire de choix plus éclairés ou d’aider vos collaborateurs à prendre de meilleures décisions.